PG电子游戏下载PG电子游戏下载无人机(UAV)是一种有动力、可控制、能携带多种任务设备、执行多种任务,并能重复使用的无人驾驶航空器。其独有的低成本、低损耗、零伤亡，具有良好的灵活机动性和隐蔽性、可重复使用和高机动等诸多优势,其使用范围已拓宽到军事、民用和科学研究三大领域。由多架小型低功耗无人机组成的无人机群可以完成多种飞行任务,而完成这些任务的基本前提之一是能够对无人机群中的每个成员进行准确的定位

　　传统的定位方法中,惯性导航系统(INS)自主性强,功能完备,但其误差随时间积累而增大;全球定位系统(GPS)提供24 h、全球、全天候的高精度的测速定位服务,但其不足之处在于自主性和可靠性差,易受干扰[3]。在复杂的飞行环境中,例如建筑物、植物、丘陵地带或者GPS接收器故障都可能导致无人机GPS观测的丢失,从而导致定位失败。在无人机编队中,不同的无人机成员之间的相对距离可以通过超宽带(UWB)无线电技术或者光学系统测得[4],有效地利用相对距离消息可以弥补INS和GPS定位的不足,从而实现无人机群的协同定位。

　　近年来,无人机群的协同定位问题得到了广泛的关注。文献[5]采用改进最小二乘算法进行三维空间中的协同定位,以参考节点为球心,以参考节点至待定节点的距离为半径的各球面相交于一点,从而能得到唯一的定位消息。但由于测距误差的存在,会使得球面交叠为一个区域或者出现不相交的情况,表现为多解或者无解[6-7]。此外,最小二乘算法的每个时刻之间独立定位,没有充分利用INS的观测信息。协同扩展卡尔曼滤波(EKF)可以充分利用INS的观测,但由于相对距离测量模型具有很强的非线性,而协同扩展卡尔曼滤波在估计中对非线性模型进行了线性化,这样就不可避免地引入了较大的线性化误差。无迹卡尔曼滤波(UKF)能以更高的精度估计非线性系统中的后验均值和协方差,因此能减少由非线性模型引起的近似误差对目标跟踪性能的影响。但是无迹卡尔曼滤波对所有高斯输入量的非线性函数进行近似,只能精确到三阶项;对于非高斯输入的近似,至少可以精确到二阶项[8]。文献[9]采用非参数信念传播算法进行定位,适用于非线性非高斯系统模型,但本身计算量非常大,主要用于二维空间的定位中。文献[10]提出的混合信念传播,性能上较前几种方法都有提高,但没有考虑和充分利用目标的运动模型和INS的输出。另外,文献[11]基于消息同步的环形交互拓扑结构提出了无人机定位方法;文献[12]考虑到移动节点的联合自定位,基于刚性图论提出了解决方法;但以上2种方法都要求距离和角度可测得,这样的要求在许多实际情况下是不满足的。文献[13]利用相对距离观测值和3个正常邻机的GPS观测对故障无人机进行联合定位,然而当故障无人机的正常邻机不足3个时,文章并没有给出解决的办法。另外也有许多基于图模型推理的传感器网络联合定位方法[14-16],然而这些方法中要求锚节点固定。但实际中,无人机正常或故障状态可能随时间变化。

　　本文提出一种基于混合动态信念传播算法的多无人机协同定位算法,主要贡献包括:

　　1) 将无人机群所有成员的状态(位置和速度)的联合后验分布用图模型描述,将无人机群协同定位问题转化为图模型上的推理问题。

　　2) 提出一种基于混合动态信念传播的分布式推理算法,该算法可以计算在给定整个无人机群到当前时刻为止的全部观测的条件下,每个无人机状态的后验分布。该后验分布的计算可以通过每个无人机对自身局部信息的处理和相邻无人机之间的消息交互来完成,无需中央处理节点,适宜于分布式实现。

　　3) 本文用高斯模型表示无人机状态的后验分布,利用粒子采样的方法实现INS消息、GPS观测和相对距离观测的融合,兼顾了参数化方法的效率和非参数化方法的灵活性。

　　本文用M表示无人机编队成员的集合。将τ时刻第i个无人机的状态记为Xiτ=(xiτ,ẋiτ),xiτ为无人机i在三维空间中的位置变量,ẋiτ为无人机i在三维空间中的速度变量。假设无人机的运动状态随时间的变化可由线性马尔可夫模型表示:

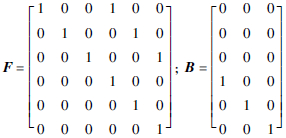
　　本文将无人机编队成员分为2类:正常无人机,即能够获得GPS观测的无人机;故障无人机,即无法获得GPS观测的无人机。用Mτn表示在τ时刻正常无人机的集合,用Mτf表示在τ时刻故障无人机的集合。随着飞行条件的变化,Mτn和Mτf中的元素会随时间发生变化。对于正常无人机,τ时刻的GPS观测模型可表示为

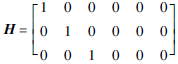
　　本文假设在一定的通信半径范围内,每个无人机成员可以获得与其他成员之间的相对距离观测。该通信范围内的无人机彼此为邻机,在τ时刻无人机i的邻机集合记为Γiτ。对于任意j∈Γiτ,相对距离测量模型为

　　式中:ζ为相对距离测量噪声,假设为零均值高斯分布,方差为σ。本文中假设相对距离观测与GPS观测相互独立。

　　本文用zMτ表示无人机编队在τ时刻产生的全部GPS观测,dM2τ表示无人机编队在τ时刻产生的全部的相对距离观测。无人机编队协同定位问题可表示为:给定当前时刻τ之前无人机编队的全部观测,计算每个无人机i位置状态的后验分布,即信念状态

　　本文用XMτ表示无人机编队全部成员在τ时刻的联合状态变量,用b(XMτ)表示无人机编队的联合信念状态。由贝叶斯公式,b(XMτ)可写为

　　式(5)表明,给定τ-1时刻的联合信念状态,τ时刻的信念状态可根据当前时刻无人机编队的观测计算而得。

　　式(5)中利用了无人机运动独立性假设、无人机运动的马尔可夫性假设和GPS与相对距离观测的独立性假设,将联合信念状态分解为因子的乘积。该信念状态可由因子图模型来描述,如2.2.1 节所示。因子图中的节点分为2类:变量节点用圆形表示,对应于无人机状态;因子节点用方形表示,对应于状态变量的因子。其中因子fi为状态变量Xτ-1i和Xτi的函数,根据无人机运动模型定义

　　因子gi为GPS观测的似然函数,对于故障无人机gi(xiτ)≡1,对于正常无人机:

　　可以看到,按上述方式定义的因子图模型与式(5)相对应,此时无人机协同定位问题转化为图模型上的推理问题。

　　本节利用混合动态信念传播算法进行因子图模型的推理,首先给出信念传播算法中各类消息的定义以及消息传递规则,然后讨论在用高斯模型近似信念状态的条件下,各类消息以及信念状态的具体形式和计算方法。

　　本文基于信念传播算法[17]进行图模型推理。信念传播算法通过图模型变量节点和因子节点之间的消息传递计算各个变量的边缘分布,从而实现每个无人机信念状态的更新。由图 1可见,图模型中传递的消息共有4种类型:①由因子fi到变量节点vi的消息mfi→vi(Xiτ),该消息反映了无人机状态的预测信息;②由因子gi到变量节点vi的消息mgi→vi(xiτ),该消息反映了GPS观测信息,只有正常无人机才能接收该消息;③由因子hij到变量节点vi(或vj)的消息mhij→vi(xiτ)(或mhij→vj(xjτ));④由变量节点vi(或vj)到因子hij的消息mvi→hij(xiτ)(或mvj→hij(xjτ))。第③、④类消息反映了相邻无人机的相对距离观测信息。注意第①类消息是关于Xiτ的分布,其余3类消息是关于位置变量xiτ的分布。

　　图 1中每个变量节点与一个无人机相对应,对于正常无人机,在τ时刻该节点通过融合来自相邻f因子和g因子的消息更新无人机的信念状态

　　对于故障无人机,通过迭代计算变量节点与h因子之间传递的消息,并更新无人机的信念状态。在第k次迭代中,首先计算相邻h因子到变量节点vi的消息:

　　在该算法中变量节点与无人机相对应,消息传递相当于相邻无人机之间的信息交互,因而,该算法可以完全分布式的实现。为了进一步提高算法性能,在实现过程中消息传递还须遵守如下规则:正常无人机不接收来自h因子的消息;故障无人机只有在接收到4个或4个以上的来自h因子的消息后,才向外发送广播消息。

　　由于相对距离观测模型的非线性,即使假定无人机初始信念为高斯分布,也不能保证后续时刻信念状态保持高斯分布形式,从而使得信念状态的解析表达变得十分困难。为了简化计算,在每一时刻用高斯分布来近似信念状态,这样无人机信念状态可完全由均值和方差2个参数刻画,信念状态的更新问题就转化为该参数的更新问题。本节将在高斯近似的前提下,讨论算法1中各类消息的具体形式及计算方法。

　　正常无人机根据GPS的观测计算消息mgi→xi,由GPS的观测模型(2)可知

　　由式(11)可知,消息mhij→vi通过因子hij和来自变量节点vj的广播消息mvj→hij相乘,并对变量xjτ进行积分而得。消息mhij→vi反映了在已知邻机位置估计及其与本机相对距离观测的条件下,对本机位置的预测信息。假设广播消息mvj→hij可近似为高斯形式,即

　　则消息mhij→vi可以看作一个球面分布,如图 2所示。该球面分布的圆心位于μxjτ,平均半径为dijτ,参数Σxjτ+σI反映了球面的厚度,σ为相对距离观测方差,I为单位矩阵。具体地,消息mhij→vi可写为如下参数化形式:

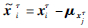
　　由式(12)可知,消息mvi→hij是由一个高斯分布mfi→vi和若干个球面分布mhij→vi相乘而得。由于球面分布的复杂性,很难给出消息mvi→hij的解析表达。因此本文假定消息mvi→hij可用高斯分布近似,借助于采样的方法计算高斯分布的均值和协方差,如算法2所示。在算法2中,首先根据mfi→vi采样N个样本{xi,sτ}s=1N,然后根据消息mhij→vi计算每个样本的权重:

　　并将权重归一化。最后由加权的样本集合计算消息mvi→hij的均值和协方差:

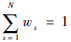
　　对于正常无人机,信念的更新由式(9)给出。由于运动模型和GPS观测模型都是线性的,以及信念状态为高斯分布的假设,正常无人机的信念更新可由卡尔曼滤波完成。根据消息mfi→vi(Xiτ)的均值式(18)和协方差式(19)计算消息矩阵

　　对于故障无人机,其信念状态由式(13)给出。可以看到,该信念状态是一个高斯分布mfi→vi和若干球面分布mhij→vi的乘积,因此可以按算法2计算该信念状态的均值和协方差。需要注意的是,在利用算法2更新信念状态时,首先要对关于Xiτ的高斯分布采样,然后根据每个样本中对应于无人机位置的元素确定样本的权重,最后按式(24)和式(25)计算故障无人机信念的均值和协方差。

　　所示。图中节点对应于无人机,无阴影的节点表示正常无人机,有阴影的节点表示故障无人机。在一个时刻内,无人机节点间的实线表示可以传递相对距离消息,箭头表示消息传递的方向,实线上的数字代表消息在当前时刻内的迭代次序,该迭代次序是由2.2.1 节所述的消息传递规则确定的。

　　Graphic of dynamic hybrid belief propagation algorithm

　　例如,标有数字“0”的从1号无人机到5号无人机的实线,表示在当前时刻内的从第0次迭代开始,每次迭代都有相对距离消息从1号无人机传递到5号无人机。不同时刻对应无人机之间的虚线代表预测消息的传递。为了简洁起见,图中没有画出节点之间的因子和GPS观测的消息,且只画出7号无人机的预测消息传递过程。

　　~图 4(f)所示,图中Iter为迭代次数。每幅图绘出了单个无人机接收到的相对距离消息,以及仅根据相对距离消息确定的无人机位置分布。在每幅图中,左上、右上和左下3幅子图分别绘出了相对距离消息被垂直于z轴、x轴和y轴且通过接收消息的无人机线个平面相切后的剖面。例如,图 4(a)中左上子图表示5号无人机在t=0时刻第0次迭代中接收的相对距离消息被垂直于z轴且经过5号无人机真实位置的平面相切后的剖面。由于相对距离消息为球面分布,所以剖面表现为环状分布。每幅图的右下子图表示仅根据相对距离消息确定的无人机位置在三维空间中的分布。

　　=0时,1号、2号、3号和4号无人机为正常无人机,5号、6号和7号无人机为故障无人机。第0次迭代时,5号无人机接收到邻机1号、2号、3号、4号无人机传来的消息,如图 4(a)所示;6号无人机接收到邻机1号、2号、3号无人机传来的消息,如图 4(b)所示;7号无人机只接收到邻机1号和4号无人机传来的消息,如图 4(c)所示。可以看到,仅根据相对距离消息,5号无人机的位置可以确定为一个高斯分布,如图 4(a)中三维图所示。而6号无人机的位置估计为双模高斯分布,如图 4(b)中三维图所示,7号无人机的位置估计为三维空间中的环状分布,如图 4(c)中三维图所示。再进行第1次迭代,5号无人机仍然接收到邻机1号、2号、3号、4号无人机传来的消息,且5号故障无人机可以发出广播消息,那么6号无人机接收到邻机1号、2号、3号和5号无人机传来的消息,如

　　所示,6号无人机可以确定自身的位置;7号无人机接收到邻机1号、4号和5号无人机传来的消息,如图 4(e)所示,该无人机的位置估计仍为双模分布。当进行第2次迭代时,7号无人机接收到足够多的相对距离消息,因而可以确定其自身的位置,如图 4(f)所示。由以上分析可以看到,通过消息传递的迭代过程,正常无人机的位置信息可以传播到整个网络,越来越多的故障无人机可以根据相对距离消息确定自身的位置。

　　可知,7号无人机在t=1时刻经过3次迭代后可以接收到来自1号、4号和5号无人机的相对距离消息,如图 4(g)所示。可以看到,仅根据相对距离观测无法确定此时7号无人机的位置。图 4(h)给出了t=1时刻7号无人机接收到的预测消息及其3个方向的剖面图。图 4(i)绘出了将相对距离消息和预测消息融合后得到的关于7号无人机的信念状态。可以看到,通过预测消息和相对距离消息的结合,可以在邻机数目不足的情况下对无人机进行准确定位。3.2 Monte Carlo仿真

　　5]和协同扩展卡尔曼滤波算法[18]的性能进行对比。在仿线个无人机在三维空间中飞行,每个无人机真实的飞行轨迹根据无人机初始状态和给定的加速度计输出序列确定。每个无人机初始位置通过在500 m×500 m×500 m大小的空间范围内随机采样确定,并假定具有相同的初始速度。无人机编队的初始状态情况为:8个正常无人机,可以获取GPS观测;10个故障无人机,没有GPS观测。随后无人机的状态会根据以下状态转换矩阵进行切换:0.90.10.10.9。其他仿真参数包括:加速度计噪声标准差为0.05 m/s

　　,正常无人机GPS观测噪声标准差为10 m;每个无人机通信范围为350 m,据此确定邻机集合;邻机间相对距离观测噪声标准差为3 m。算法1中迭代次数取为3,算法2中的采样粒子数目为100。算法的主要性能指标包括:每个时刻下无人机平均位置误差,其定义如下:

　　中纵坐标为所有无人机的平均位置误差,横坐标为时间步进(无量纲),每段时间步进内,无人机组切换状态,按设定的迭代次数与采样粒子数执行算法,完成所有无人机的定位。可以看到,由于改进最小二乘算法没有利用加速度计的输出信息,同时由于编队中正常无人机数目较少,使得该算法误差较大,且波动较为明显。对于协同扩展卡尔曼滤波算法而言,由于有效地利用了运动模型约束,定位精度较改进最小二乘算法有大幅提高,但由于算法对非线性观测模型进行了低阶近似,所以仍存在一定的误差。而本文提出的混合动态信念传播算法不仅考虑了运动模型的约束,同时用参数化模型表示相对距离消息的球面分布,并且通过粒子采样实现不同分布形式的消息间的信息融合,从而得到了更高的定位精度。

　　图 6给出的误差-比例曲线,横坐标表示不同的位置误差,纵坐标表示位置误差小于横坐标上对应误差值的无人机数量占总无人机数量的比例。从图 6可以看出,对任意给定的无人机位置误差限制,采用本文算法得到满足该定位精度要求的无人机数量总是大于或等于其余2种算法。

　　图 7(a)所示,灰度值整体偏低,说明定位精度较高。图 7(b)中改进最小二乘算法定位效果则不稳定,随着时间的变化位置误差的波动性较大。图 7(c)中协同扩展卡尔曼滤波呈现出来的灰度都偏白,说明定位精度不是很高,基本在10 m左右的水平。

　　Each UAV position error variation with time

　　无人机的定位性能还受到许多因素的影响,包括飞行编队中正常无人机所占比例、无人机之间的通信距离、GPS观测噪声以及相对距离值观测噪声。本文通过仿真对上述因素对无人机定位性能的影响进行了对比研究,如

　　所示,纵坐标表示无人机位置估计的平均误差,横坐标对应于不同影响因素的变化,每幅图的数据是对10次Monte Carlo仿真结果求平均后的结果。

　　Normal UAVs quantity ratio-position error curves

　　Communicate range-position error curves

　　Relative distance noise-position error curves

　　正常无人机在联合定位中起着十分关键的作用,正常无人机数量的改变对各个算法性能的影响结果如

　　所示。在仿真过程中,无人机正常或故障的状态不再进行切换,其中横坐标表示正常无人机在飞行小组内所占比例,纵坐标表示无人机的位置估计误差。从

　　可以看出,改进最小二乘算法和协同扩展卡尔曼滤波算法性能受到正常无人机数量的影响较大,在正常无人机数量十分稀少的情况下,2种算法都具有较大的估计误差。本文提出的混合动态信念传播算法,能够在正常无人机数量较少的情况下,先确定正常无人机邻机位置,然后通过信念的传播依次确定其他故障无人机的运动状态,因此正常无人机所占比例对算法性能影响明显小于传统的2种算法。当正常无人机数量减少到4个(保证所有故障无人机运动状态估计精度的最少数量)的时候,本文算法得到的估计误差在8.5 m左右。无人机之间的通信距离是另一个影响算法性能的重要因素。无人机之间在每一时刻的连接关系是由该时刻下的无人机的真实位置和通信范围决定的。通信范围的变化对各个算法性能的影响如

　　所示,可见,在通信范围较小的时候,无人机之间可通信的邻机数量很少,各个算法对于无人机的运动状态的估计误差都较大。但此时本文算法和协同拓展卡尔曼滤波算法明显优于改进最小二乘算法。而当通信距离逐渐增大时,3种算法的定位精度均有所提高。

　　所示。在噪声不断增大的过程中,3种算法的位置误差都随之增大。改进最小二乘算法的误差的来源是GPS观测噪声和相对距离观测噪声,所以其位置误差对这2类噪声的依赖性很大,可见其曲线的增长幅度较大。而协同扩展卡尔曼滤波算法和本文算法,由于利用了加速度计的输出,定位精度对GPS观测噪声和相对距离观测噪声的敏感度有所降低。而本文所提算法的性能始终优于其他2种算法。

　　通过仿真实验,综合影响定位性能的各项要素,本文算法显示出异于传统算法的优越性,但出于实际应用考虑,其稳定性与普适性更应加以提升,所以,该研究尚存在以下局限与不足:

　　1) 仿真实例中简化了无人机编队飞行网络,该算法假设各个无人机的运动相互独立。然而很多情况下,无人机之间的运动是相互关联的。

　　2) 考虑到节点通信能力的限制,本文采用的分布式实现,可有效避免集中式分布中因节点通信过载而导致的网络崩溃;但同时,该分布式在线估计仿真实验环境还处于较为理想的状态,实际网络节点的连接有时十分稀疏。

　　本文提出了一种基于混合动态信念传播的多无人机协同定位算法。该算法能够在部分无人机GPS观测丢失、无人机之间的通信范围较小等情况下,对无人机进行准确的定位。在此深入探究过程中,主要成果有:1) 建立无人机运动模型、GPS观测模型和相对距离观测模型,表述与转化定位问题为信念状态的求解。2) 利用运动的马尔可夫性质及节点间的运动独立性,基于贝叶斯公式,因式化无人机组联合信念状态,由此建立了因子图模型。

　　4) 在仿真与验证试验中,该算法与传统算法做出比较,证明了本文算法的有效性与准确性。为使本文算法更加完善,仍需要进一步用图模型描述无人机之间运动的相关性,开发相关推理算法估计无人机的状态;加入不同任务数据可信度标识方面的研究工作,以应对无人机组任务分化状况;并考虑数据关联问题,以收敛位置误差。