
2025-06-15
分享到
【三维路径规划】基于粒子群算法融合鸡群算法多无人机三维路径规划含Matla
1 简介 粒子群优化算法 (particle swarm optimization, PSO)是Kennedy和Eberhart于1995年提出的一种群体智能仿生算法, 在解决一些典型的函数优化问题时, 能够取得比较好的优化结果。 **1 无人机航迹
一般地, 无人机航迹规划的空间可以表示为某三维坐标系下所有点的集合{ (x, y, z) xmin≤x≤xmax, ymin≤y≤ymax, zmin≤z≤zmax}, 其中x, y可以表示为该节点在飞行水平面下的坐标, 也可以表示为该点的经纬度, z为高程数据或海拔高度。航迹规划的目的是获得无人机在该空间中的飞行轨迹, 生成的航迹可表示为三维空间的一系列的点{PS, P1, P2, …, Pn-2, PG}, 相邻航迹点之间用直线段连接。
式中, s表示航迹段数, Li表示第i段航迹长度, 该项代表距离代价。Hi表示第i段航迹的平均海拔高度, 该项代表高度代价。Ti为第i段航迹的威胁指数, 该项代表威胁代价。k1、k2、k3分别是距离代价、高度代价和威胁代价的权重值, 权重的选取与飞行任务要求相关。
粒子群算法初始化为一群数量为N的随机粒子 (随机解) , 在D维空间中通过重复迭代、更新自身的位置以搜索适应度值最优解。粒子的位置代表被优化问题在搜索空间中的潜在解。在每次迭代中, 粒子通过跟踪2个“极值”来更新自己的速度和位置:一个是粒子自身目前所找到的最优解, 即个体极值;另一个是整个粒子群目前找到的最优解, 即全局极值。粒子i (i=1, 2, …, N) 在第j (j=1, 2, …, D) 维的速度vij和位置xij按如下格式更新:
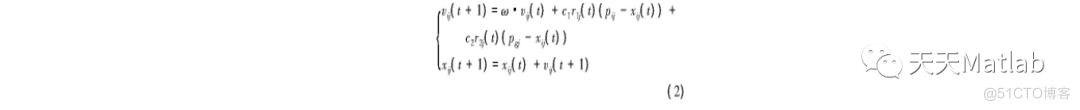
式中, ω为非负数, 称为惯性权值 (惯性因子) , 描述了粒子对之前速度的“继承”, 即体现出粒子的“惯性”;c1和c2为非负常数, 称为学习因子 (加速因子) , 体现了粒子的社会性, 即粒子向全局最优粒子学习的特性;r1和r2为 (0, 1) 之间的随机数;pi= (pi1, pi2, …, pi D) 表示粒子i的个体极值所在位置;pg= (pg1, pg2, …, pg D) 表示所有粒子的全局极值所在位置。
速度更新公式的第一项, 反映粒子当前速度的影响, 每一个粒子按照惯性权值的比重沿着自身速度的方向搜索, 起到了平衡全局的作用, 同时避免算法陷入局部最优;第二项体现了个体最优值对粒子速度的影响, 即粒子本身的记忆和认识, 使得粒子具有全局搜索能力。第三项则反映群体对个体的影响, 即群体间的信息共享起到加速收敛的作用。
上一篇:【三维路径规划】基于模拟退火算法结合粒子群算法多无人机三维路径规划含
【三维路径规划】基于粒子群算法融合鸡群算法多无人机三维路径规划含Matla
【图像隐藏】基于DCT和FFT数字水印嵌入+攻击+提取含Matlab源码
【优化调度】基于NSGA2算法多技能员工调度优化模型含Matlab源码
【ElM分类】基于麻雀搜索算法优化ElM神经网络实现数据分类附matlab代码
#yyds干货盘点#upper、lower字符大小函数 - python基础学习系列(33)
【麻雀搜索算法】基于Circle混沌麻雀搜索算法求解单目标优化问题matlab代码
#yyds干货盘点#upper、lower字符大小函数 - python基础PG电子免费试玩